On trouve sur nos toits ou nos blacons des antennes pour recevoir la
télévision par satellite, qu'on appelle « antennes
paraboliques » ou même « paraboles ». Mais
d'où vient ce nom ? |
 |
|
|
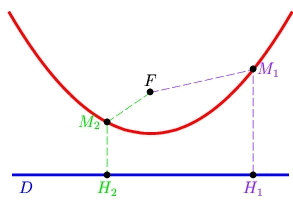
Il faut tout d'abord définir ce
dont on parle : une parabole est l'ensemble des points
situés à la même distance d'un point F (le foyer) et d'une
droite D (la directrice). Cela signifie qu'un point
M appartient à la parabole si (et seulement si) la
distance MF est égale à la distance
MH où H est le projeté
orthogonal de M sur D. |
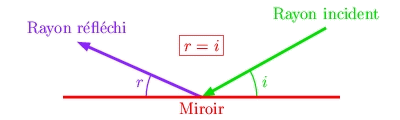
Quand une onde vient frapper la surface de l'antenne, elle est réfléchie comme le sont les rayons lumineux sur un miroir. Ce phénomène est décrit par la loi de Descartes. La figure ci-contre montre le trajet d'un rayon lumineux quand il percute un miroir plan : l'angle i est appelé angle d'incidence; r est l'angle de réflexion. La loi de Descartes affirme que ces deux angles sont égaux. |
 |
|
|
La loi de Descartes s'applique aux miroirs plans, dont notre antenne
parabolique ne fait justement pas partie... Alors, on jette ?
Évidemment pas. La réflexion s'opère comme si on
remplaçait l'assiette parabolique de l'antenne par un miroir
plan. Mais pas n'importe quel plan : précisément celui qui
est le plus proche de l'assiette autour du point
d'impact. |
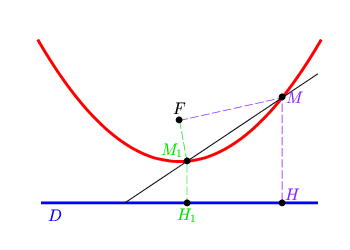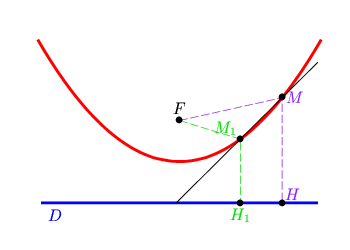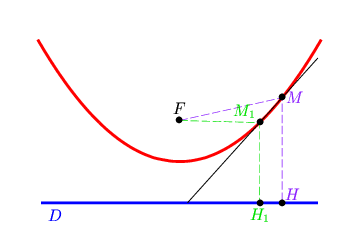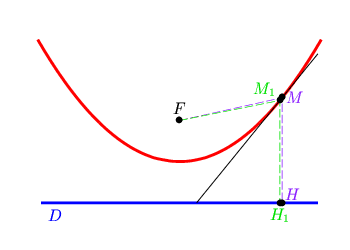
Mais comment tracer cette droite tangente ? Dans la figure ci-dessus,
le point M est situé sur la médiatrice
du segment [FH] (car les distances
MF et MH
sont égales). De la même façon,
M1 appartient à la médiatrice de
[FH1]. Ainsi la droite (
MM1) se rapproche de la
médiatrice de [FH] au fur et à mesure
que le point M1 tend vers le point
M.
L'explication qui précède est difficile car elle fait
intervenir la notion de limite qui est délicate (tout peut être
justifié, mais il faut des connaissances mathématiques que le
lecteur n'est pas supposé avoir). Il faut retenir
que tout se passe comme si on remplaçait la parabole par sa
tangente au point d'impact du rayon et que la tangente en un point
M est la médiatrice du segment [FH].
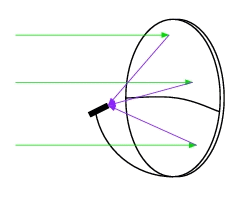
Dans le schéma qui suit, on a dessiné en vert un rayon incident qui arrive perpendiculairement à la droite D (le directrice de la parabole). La tangente en M a été représentée en noir. Le triangle MFH est isocèle en M si bien que la tangente est, non seulement la médiatrice du segment [FH], mais aussi la bissectrice de l'angle FMH. On en déduit que les angles r et j sont égaux. De plus, les angles i et j sont opposés par le sommet, donc égaux. Finalement, les angles i et r sont égaux ce qui prouve, à l'aide de la loi de Descartes, que la direction (MF) est celle du rayon réfléchi.

Notre démonstration prouve que tout rayon arrivant dans la
direction perpendiculaire
à la directice se réfléchit au
foyer F. |
 |
L'étude qui précède est une belle application de la géométrie dans la vie quotidienne. On s'aperçoit que les outils qu'on apprend en maths dès la classe de 4e n'ont pas qu'un intérêt théorique. Leur portée est en fait bien plus grande que ce qu'on en a présenté ici : la géométrie intervient partout. Les profils aérodynamiques des voitures et des avions, par exemple, sont calculés grâce à des maths très savantes. De la même façon, demandez-vous pourquoi les cheminées de refroidissement des centrales électriques ont des formes si bizarres, alors qu'il aurait été si simple de les construire cylindriques...
On peut retrouver le résultat qu'on a démontré ici par une méthode géométrique à l'aide d'une technique analytique. Cet exercice est accessible aux élèves de terminale : il suffit de savoir que l'équation d'une parabole est de la forme y=p.x2. A vos crayons !
La parabole n'est pas la seule courbe à posséder des propriétés de réflexion intéressantes. L'ellipse est tout aussi remarquable. Elle comporte deux foyers; un rayon issu de l'un d'entre eux se réfléchit dans le deuxième. On peut en voir une application à l'abbatiale de la Chaise-Dieu dans la Haute-Loire : une des salles possède une voûte elliptique qui servait à la confession des lépreux. Le malade parlait face à un mur juste à l'endroit d'un foyer et son confesseur se trouvait à une quinzaine de mètres à l'autre foyer et entendait parfaitement les sons qui lui parvenaient, même émis à voix basse. Les parisiens pourront aussi essayer de se parler d'un quai à l'autre à voie basse dans certaines stations de métro...
- Une page intéressante de l'IREM (Institut de Recherche en
Enseignement des Mathématiques) sur les miroirs paraboliques.
http://chronomath.irem.univ-mrs.fr/Courbes/miroirpara.html. - Étude de l'ellipse et de ses propriétés de
réflexion.
http://perso.club-internet.fr/rferreol/encyclopedie/courbes2d/ellipse/ellipse.shtml. - Un site sur l'origine des termes mathématiques, entre autres
parabole et ellipse.
http://perso.club-internet.fr/rferreol/langage/notations/notations.htm.
|
|
|