Partie B:
3-Symétrie de l'implosion ou...
Comment limiter les instabilités de plasma ?
Comment limiter les instabilités de plasma ?
|
|
Partie B:
3-Symétrie de l'implosion ou...
Comment limiter les instabilités de plasma ? |
|
Les flux intenses reçus par la cible rendent l’implosion de celle-ci très sensible aux instabilités hydrodynamiques. Maintenir une symétrie d’éclairement, donc de poussée ainsi que la plus parfaite sphéricité initiale de la cible sont des impératifs indispensables à la non pollution thermique du combustible et donc à l’obtention de l’ignition.
3.1.Les instabilités hydrodynamiques
Elles sont nombreuses et leur étude encore en cours aujourd’hui : si l’ignition devait ne pas être atteinte en laboratoire, c’est essentiellement à cause des conséquences de ces multiples instabilités. Ce sont elles qui rendent également à priori impossible l’aboutissement de la 2ème grande voie de fusion : la fusion magnétique à cause de la nécessité de temps de confinement longs vu les faibles densités, laissant ainsi le temps à ces instabilités de s'amplifier !
Elles ont pour principale conséquence de créer des petits courants de convection qui "diluent" la chaleur au sein de l'ensemble du combustible au lieu qu'elles soit concentrée au niveau du point chaud. Ainsi l'ignition ne peut être amorcée au point chaud et à fortiori dans le reste de la cible.
La plus importante d’entre ces instabilités et la seule étudiée dans ce dossier est celle de Rayleigh-Taylor . On ne fera que citer les autres pour en montrer l’éventail : RT, T-Birkhoff, Richtmyer-Meshkov, Kelvin-Helmholtz dont les phases successives dans le temps (linéaire, quasi linéaire, chaotique et turbulente) correspondent à des amplitudes croissantes de défauts.
3.2.1.Définition
Ces instabilités se manifestent lorsque un milieu léger pousse ou freine un milieu lourd : elles se manifesteront dans la phase d’accélération et de décélération de la cible lors de l’implosion, et ce à chaque interface entre 2 milieux rencontrée lors de la propagation de ces instabilités.
Il existe 4 interfaces susceptibles d’être instables dans notre configuration
de cible choisie
3.2.2.Propagation des défauts : conséquences
On voit alors tout l’intérêt de partir d’une configuration de cible la plus sphérique possible et maintenir une uniformité d’éclairement la plus parfaite afin d’éviter l’amplification de défauts qui amènerait d’une part un percement de la coquille donc une pollution du DT et une compression insuffisante et d’autre part un mélange DT chaud / DT froid empêchant l’allumage.
Le document ci dessous montre de façon schématique l’amplification des
défauts au niveau des différentes couches de la cible. Tout d’abord au niveau
du front d’ablation où les rugosités de l’ablateur s’intensifient provoquant
un percement de la coquille et ensuite au niveau de l’interface DT solide –
DT gazeux entraînant un préchauffage du DT froid et donc éteinte de l’ignition.
 |
|
Les phases instables lors d'une
implosion
|
Il est à remarquer que jusqu’ici on a dit qu’il était bon de prendre le RAV le plus grand possible pour augmenter le rendement hydrodynamique et diminuer la température de cavité et donc l’énergie à investir pour atteindre l’allumage. Or on voit apparaître ici la nécessité de ne pas prendre un RAV trop grand car , à quantité de combustible et d’ablateur fixées, si R(coquille) augmente alors ΔR diminue ; et une coquille fine est plus sensible aux instabilités et perce plus facilement, de même qu’une épaisseur plus faible de DT froid entraîne un plus grand risque de préchauffage.
On va voir dans le paragraphe suivant les meilleurs compromis à considérer
3.2.3.Traitement analytique de la propagation des défauts pour les instabilités RT
On se limitera à la seule étude des instabilités au front d’ablation qui sont les plus importantes !
Les instabilités de RT correspondent à une croissance linéaire dans le temps des défauts : c’est le modèle de Takabé.
On classifie les différents défauts en modes (notés L). Ce paramètre L peut être assimilé au nombre de lobes de la déformation : L = k.R(t) dans le cas d’une sphère où k= 2π/λ
L’amplitude
a d’un défaut s’exprime alors comme :
 |
 |
| g = accélération de la pesanteur |
| ε est un facteur traduisant l'influence de la longueur du gradient de densité et de la vitesse relative du front d'ablation |
Soit Ri et Rf les positions initiales et finales du front d’ablation, alors Ri - Rf représente la distance parcourue par par la partie non ablatée de l’ablateur donc par l’extérieur du combustible,soit : Ri - Rf = gt2/2 =R/2 (pour fixer les idées)
La condition de non percement de la coquille s’exprime par : a(t) < &DDelta;R (épaisseur de la coquille)
On ne considère que le mode le plus dangereux à savoir celui correspondant à λ = ΔR
D'où
 |
 |
 |
Là encore le RAV apparaît comme un critère essentiel ; de son choix dépendera l’aboutissement ou non de l’ignition. On voit nettement apparaître une limite supérieure pour le RAV si l’on veut restreindre l’effet des instabilités de type RT.
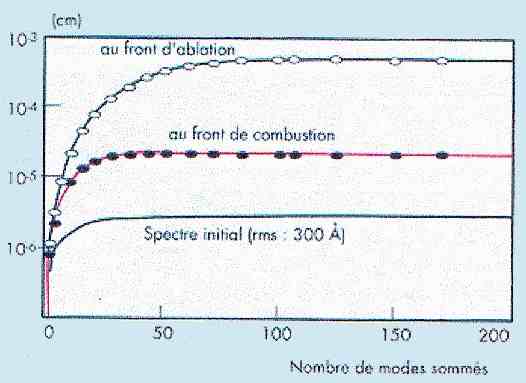
Pour prendre en compte l’ensemble des modes d’amplitude existants, on somme les amplitudes a(t) sur tous ces modes. La courbe suivante montre bien l’amplification des défauts à la fois au front d’ablation et au front de combustion où le point chaud risque d’être pollué et l’ignition s’éteindre.
 |
|
Croissance des défauts de sphéricité selon le modèle de Takabé en fonction du nombre de modes sommés revue CHOC N°13 |
Etude
d’un cas concret permettant d’apprécier l’influence de 2 paramètres : RAV
et rugosité initiale :
On considère:
2 RAV, un «petit »
et un «grand»
2 rugosités initiales
de l’ablateur, une faible (0.03 mm) et une forte (0.15 mm)
|
 |
||||||||||||||||||||
|
|||||||||||||||||||||
|
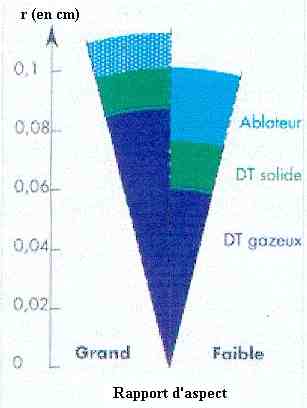
schématisation de 2 cibles de RAV différents
|
|||||||||||||||||||||
|
Comportement de 2 cibles
vis à vis des instabilités de RT
|
|||||||||||||||||||||
On constate alors que le seul cas où ,en fin d’implosion , l’amplitude de la déformation est inférieure à l’épaisseur restante d’ablateur est le cas faible rugosité et faible RAV : alors seulement il n’y aura pas percement de la coquille !
a(R+dR) = a.exp(- k.dR)
Comme R diminue au cours du temps , k = L/R(t) augmente pour un mode donné
On devra donc prendre garde à ce que k.dR soit assez grand , typiquement > 1
La distance entre les 2 fronts (ablation/allumage) = ΔRc = épaisseur des matériaux denses
k.Δ Rc > 1 soit L.(ΔRc/R) > 1 ,c'est à dire: R/ΔRc devra être le plus petit possible, de sorte que tous les modes de déformation satisferont la condition de non propagation des défauts au front de combustion..
|
|
|
|
N'hésitez pas à |