Partie B : 2-Implosion du micro-ballon

Nous allons voir comment comprimer le micro ballon en mettant en vitesse centripète la partie solide de la coquille qui sert  de piston pour mettre en condition le DT et permettre l’ignition.

 2.1.Régime du pousseur explosant                                       

Dans le cas où le libre parcours moyen des X (λ_x) ,est supérieur à l’épaisseur de la coquille (quelques microns) , le dépôt d’énergie des X se fait dans toute l’épaisseur de la coquille qui explose alors symétriquement, la partie interne mettant en vitesse centripète le combustible.

La compression est ainsi très rapide et l’explosion très symétrique d’où une limitation des conséquences des instabilités de type R-Taylor (cf  partieB 3.2) . Cependant dans ce type d’explosion de la coquille, cette dernière ne fait rapidement plus écran de sorte que les X viennent chauffer directement le combustible dont la pression interne augmente et s’oppose à sa compression. La densité finale du DT solide ne pourra être très élevée et il faut donc adopter une autre manière de comprimer le DT.

 2.2.Régime ablatif                                    

            Cette fois, on fait en sorte que λ_x< ΔR : on augmente l’opacité de la coquille aux rayons X.Pour ce faire, on peut soit accroître l’épaisseur de la coquille mais pour des X très énergétiques type mégajoule, cela nécessiterait des épaisseurs beaucoup trop importantes. On a alors recourt à des coquilles (appelées désormais ablateur) de Z faible (CH) dopé avec un matériau d’opacité adéquate (Z élevé).

                        Le dépôt d’énergie n’a lieu dans ce cas qu’en périphérie ; la partie de l’ablateur ainsi chauffée se trouve éjectée vers l’exterieur et ce dernier est grignoté petit à petit. Par effet fusée le combustible et la partie restante de l’ablateur sont comprimés sous l’effet de la mise en vitesse centripète. Et dans ce cas de figure il reste toujours une épaisseur d’ablateur telle que la compression se réalise sans préchauffage du DT froid .

                La figure ci dessous résume le mécanisme d’implosion de la micro cible : on voit bien l’éjection des déchets de l’ablateur vers l’extérieur au cours du temps, càd au fur et à mesure que le laser y dépose son énergie ; la compression progressive puis brutale du combustible jusqu’à des ordres de grandeur permettant l’ignition par rayonnement du point chaud dans le DT froid et très dense. On peut remarquer que la dernière zone de compression est une zone de forte accélération (puis deccélération lorsque la pression interne s’oppose à la compression ), donc une zone où pourront se développer de fortes instabilités de type R-Taylor (cf partieB 3.2).

Schéma d’évolution des rayons des constituants de la cible en fonction du temps lors de l'implosion revue CHOC N°13

2.3.Mise en forme de la loi de poussée

2.3.1.Rapport d’aspect en vol , caractéristique de la cible

                        Il existe un paramètre simple permettant de qualifier un grand nombre d’autres paramètres relatifs à la vitesse , à la symétrie d’implosion , mais aussi à la sensibilité aux instabilités de plasma ; autant dire qu’il est fondamental : c’est le rapport d’aspect en vol, (noté RAV) . Il se définit comme : R/ΔR (rayon de sphère sur son épaisseur). On verra au fur et à mesure comment le choisir.

                         En 1^er lieu, deux considérations semblent indiquer qu’il faille le prendre le plus grand possible :

• En fait l’énergie communiquée à la capsule &cong; P * ΔV 

                       ΔV = Vⁱ - V^f est la différence entre le volume initial de la sphère et son volume en fin d’implosion

   Donc à masse de combustible fixée, plus RAV est grand, plus ΔV est grand puisque le paramètre important est l'état de compression finale du mélange qui permettra d'atteindre l'ignition : si l'on part d'un grand volume initial, la différence de volume entre le début et la fin de la compression sera d'autant plus grande. Et plus ΔV est grand, plus la pression (P) à exercer est faible

   Or une formule empirique donne P=a *(T_r )^b  avec b= 3.4 et T_r= température radiative    

  Donc un RAV grand conduit à une température radiative (celle des X) à atteindre beaucoup plus faible, soit encore une énergie laser à investir diminuée d’autant.

• De même , pour accroître le rendement hydrodynamique ( G₄ = E _{interne DT} / E_{X absorbée}), on choisira un grand RAV :
  G₄(%)= 4,4 .(R/ΔR)^0,3 . α^0,18 ≅ 15%, le paramètre α caractérise l’entropie donc le préchauffage.

2.3.2.Loi de poussée

                        Des simulations numériques ont montré que pour obtenir l'ignition, on devait atteindre une température radiative de l'ordrede T_r=3.10⁶ K (pour un RAV moyen de l’ordre de 30), d’où P= 10⁴ Gpa = 10⁸ bars

                        Si cette pression était appliquée brutalement , le choc induirait une forte augmentation  d’entropie donc le DT froid s’en trouverait préchauffé et son agitation thermique donc sa pression cinétique interne augmentera, d’où limitation de la compression et non atteinte de l’ignition. Typiquement le gain de la cible G₃=1,35.(E_DT/α³)^0,3. Donc si l'entropie augmente, le gain de cible chute (l'entropie est au dénominateur et la puissance 3) .

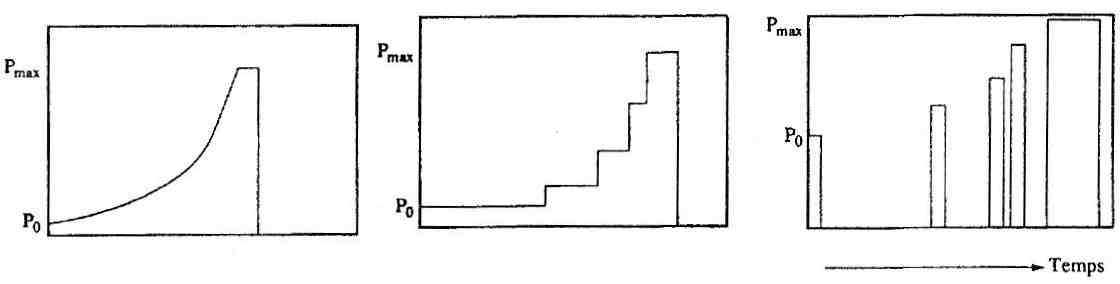
                        On devra donc appliquer la pression et donc la température par paliers successifs avec une chronométrie adaptée à la création du point chaud. La figure suivante donne une idée des différentes formes des lois de pression qui pourraient convenir pour comprimer le mélange sans le préchauffer (gain de cible constant).

Diverses formes de loi de poussée en fonction du temps Hydrodynamique et implosion, Dautray et Watteau, Eyrolles 1993

  2.4.Formation du point chaud                                                   

• schéma classique :le DT solide qui doit rester froid est comprimé sur une isentropique basse, ce qui nécessite un parfait synchronisme des chocs. Le centre du DT gazeux est placé dès le début sur une isentropique haute puis comprimé jusqu’au domaine d’allumage. Ce phénomène s’explique par le rapport des densités existant entre DT solide et gazeux : le passage du choc initial du DT solide au DT gazeux provoque la « montée » de ce dernier sur une isentropique haute !



Schéma classique d'allumage dans le plan Températue-densité surfacique revue CHOC N°13



• allumeur rapide :  l’ensemble du combustible est comprimé par le laser principal selon le mécanisme étudié auparavant puis on utiliserait 2 lasers ultra-brefs et ultra-intenses : un d’une durée d’une dizaine de pico-secondes dont le but est de créer un canal vide  à travers la couronne dense de DT ( ce grâce à des mécanismes n’apparaissant qu’à très forte intensité et qui requièrent encore de nombreuses études théoriques), et un autre d’une durée encore plus courte qui passera à l’intérieur de ce canal pour venir chauffer le combustible central et créer ainsi un point chaud.
  

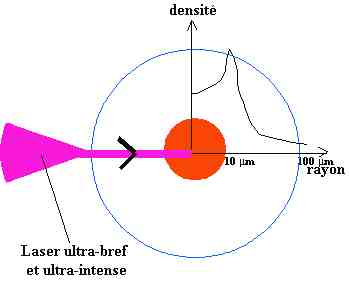
  Schéma de l'allumeur rapide dans le plan Température-densité surfacique revue CHOC N°13	Allure de la densité du point chaud en fonction de la distance au centre de la cible R.Goutallier 2001

  
  

                          L’énorme avantage conceptuel de ce pico-allumeur est de rendre la cible beaucoup moins sensible aux phénomène de préchauffage donc aux instabilités de plasma.

N'hésitez pas à m'écrire pour des critiques (constructives) ou des renseignements