Partie A: 2-Modélisation progressive de la fusion du DT

2.1.Nécessité de confiner le plasma               

Aux températures où l’on va porter notre mélange, toute la matière sera ionisée : on obtient un plasma constitué de 3 gaz (e-,D,T).Dans un plasma chaud les ions parcourent de grandes distances avant de subir la fusion : libre parcours de fusion = 1/nσ = 10¹⁰ cm .On ne peut donc permettre aux particules de rebondir sur les parois d’une cavité quelconque sans quoi elles perdraient une grande partie de leur énergie et la fusion serait stoppée.

            Il est donc indispensable de confiner les particules pendant un temps permettant à une fraction notable de combustible de fusionner. Dans le cas qui nous intéresse, c’est l’inertie de la matière qui réalise le confinement. Un éclairage intense (laser ou X) et uniforme comprime une petite sphère cryogénique de DT qui atteindra ainsi les conditions de fusion et se désagrégera en un temps très court (limité par l’inertie) mais suffisant pour permettre un dégagement notable d’énergie : on notera désormais t_r ,le temps de confinement autrement dit le temps durant lequel le Deutérium et le Tritium peuvent réagir.

2.2.Gain de la réaction et de l'installation                                           

2.2.1.Définition pour la totalité de l’installation

                        Le but de la fusion est de dégager de l’énergie thermonucléaire (E_fusion = E_f) à partir d’une énergie laser investie (E_laser). On définit un gain global  pour l’installation (noté G) : G = E_recup / E_{electre utilisée}              

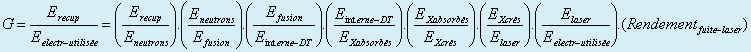Avec G_i les rendements aux différentes étapes du processus de fusion du mélange DT :

• G₁ = E_recup / E_{des neutrons} = 0.3 à 0.5 , cycle thermique
• G₂ = E_{des neutrons} / E_f = perte de l’énergie des α mais qui permet l’ignition= 100% dans une couronne de DT très dense.
•  G₃ = Q = E_f / E_{interne DT} = gain de la cible                      
• G₄ = E _{interne DT} / E_{X asorbés} = rendement hydrodynamique de transfert de l’énergie au combustible = 0.15 à 0.2  
• G₅ = E_{X absorbés} / E_{X crées} = rendement de l’absorption des X
• G₆ = E_{X crées} / E_laser = rendement de conversion X @ 90% avec une l = 0.35 μm pour le laser
• G₇ = E_laser / E_{electr  utilisée} = 0.2 à 0.3    
    
• G₈ = fuites lasers (g=0.95) et réinvestissement de l’énergie électrique (g=0.85)=0.8

                        Pour obtenir un gain d’installation convenable (G>10 ), il importe de choisir des configurations de cible à haut gain (G₃ >100 voire 1000) : on a grossièrement G = 0,015.G₃

2.2.2.Evaluation du gain du combustible à T et densité constantes

               Pour un mélange equimolaire de DT, le nombre de particules par unité de volume est :   n_D = n_T = n/2 ,d’où le nombre de fusion (noté N_f) par unité de temps et pour un volume V est donné par :    

Où <σv> est la moyenne selon une statistique de Maxwell- Boltzmann du produit de la section efficace de la réaction avec la vitesse relative des particules . Dans le gaz à température T , la distribution des vitesses selon MB s’exprime :

On obtient donc en faisant une intégration sur les distributions de vitesse à la fois du Deutérium et du Tritium :

            L’énergie dégagée par la fusion pendant un temps de confinement donc de combustion t_r s’exprime comme :               

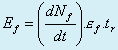            où  ε_f = énergie dégagée par une réaction de fusion

car les températures ionique et électronique sont égales dans le plasma.

On en déduit le gain du combustible G₃  :

         On peut alors définir un critère théorique donnant un gain G’ = G(1)*G(3) > 1 

Ce critère est appelé critère de Lawson et n’est cité ici que pour des raisons historiques car il est évident qu’il ne représente pas grand chose dans notre problème. En effet il n’inclut que le rendement du cycle thermique et ne s’occupe pas de se qui se passe en amont (comment est initié la réaction de fusion). De plus avec un G > 1 , on atteindrait un bilan d’énergie positif mais en aucun cas une installation industrielle rentable ! On donne tout de même le critère de Lawson :

                                               n.t_r > 10¹⁴ s/cm³  avec T = 2,3.10⁸ K

            Enfin on utilise essentiellement nt_r pour caractériser la fusion magnétique et non la fusion inertielle pour laquelle nous utiliserons le critère ρR caractérisant la cible. En effet :

                                   n_i= ρ /<m_i> où  <m_i> est la masse moyenne des ions , et

            t_r= temps mis par la sphère de rayon R pour se désagréger sous l’effet de la pression interne , on admet alors pour simplifier la modélisation que t_r = R/v_s où v_s est la vitesse du son à la température T

                                               v_s = c_s * T^1/2       c_s = 2.10⁵ m s^-1 keV ^-1/2

                        On obtient ainsi le gain G₃  de façon plus explicite pour la fusion inertielle 

On voit ainsi que le gain de cible est directement relié à certaines caractéristiques de celle ci (son rayon, R et la masse volumique atteinte lors de la compression, ρ) que l'on s'efforcera de bien choisir pour obtenir un gain de cible élevé.

 ce gain de cible est maximum à T=18 keV pour une valeur de ρR fixée

                         Cependant, toujours à ρR fixé , l’énergie à fournir pour porter le DT à cette température est proportionnelle à sa masse soit ρR³ d’où l’intérêt de travailler à des densités élevées pour augmenter le gain de cible en gardant l'énergie à investir constante, augmentant de fait l'énergie récupérée. Ce sera le principal objet de la partie B., comment comprimer le mélange ?

2.2.3.Température et densité non constante :facteur de réduction

Même si t_r <<1, T et ρ ne sont pas constantes car la détente du milieu provoque une augmentation du rayon de la sphère. Cependant , on admettra que T et ρ sont uniformes au sein du combustible .

           Ainsi par rapport au cas où on ne considérait pas la détente, le nombre de molécules fusionnant N_f  s’en trouve réduit d’un facteur Y = 1 / [3(γ -1)(B-1/2) + 2], de même que le temps de confinement et par conséquent le gain de la cible G₃ . Numériquement, à 20 keV, Y = 4 ; l’obtention de gains élevés s’éloigne d’autant.

2.2.4.Raréfaction du combustible

                        Il existe un autre facteur limitant la réaction. En effet la densité du milieu diminue sous l’effet de la détente mais aussi sous celui de la raréfaction du combustible à moins que le taux de combustion (noté f_c ) soit négligeable , ce qui n’est pas précisément le but recherché !…
                       On démontre en annexe 2  l’expression du taux de combustion du mélange :

On remarque qu’il est fonction de (ρr)_initial et d’une fonction de la température KA(T)

La courbe que l’on en déduit est assez parlante :

	Ainsi pour, à 10 keV, ρR = 1 kg/m2 , fc << 1                                                            ρR = 100 kg/m2 , fc = 30% ce qui est acceptable au point de vue de la rentabilité. Il apparait la encore que l'on doit prendre un facteur ρR élevé pour augmenter le taux de combustion (donc G3). Nous relativiserons cet argument dans la partieB-3 dédiée à l'étude des instabilités hydrodynamiques lors de l'implosion.
Taux de combustion en fonction des paramètres de la cible
Hydrodynamique et implosion, Dautray et Watteau, CEA

                  Enfin, on donne les courbes de gain de cible dans le plan Température- densité surfacique :  

(résultat démontré en annexe 3 )

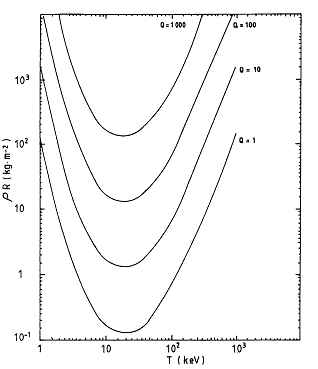	On remarquera qu’elle présentent toutes un minimum aux alentours de 30 keV , cette température représente donc la façon la plus économique d’obtenir un gain de cible (G3 ici noté Q) fixé.
Gain de cible (G3) dans le plan température-densité surfacique
Hydrodynamique et implosion, Dautray et Watteau, CEA

2.2.5.conclusion

                Finalement le taux de combustion augmente de façon monotone avec ρR et tend vers 1 pour les valeurs élevées de ρR. Il faudrait ainsi des valeurs de ρR de l’ordre de 400 kg/m²  pour avoir des taux de combustion de 50% (à T=10keV) et donc des gains de cible G₃ supérieur à 100. Or cette valeur de ρR n’est pas réaliste car si l’on considère une cible de rayon 100 mm (cf A-II-4 pour le dimensionnement de la cible), cela conduit à ρ=4.10⁶ kg/m³ soit près de 10 000 fois la densité de l’état solide du mélange !(ρ_solide= 200 kg/m³)

            Aussi va-t-on améliorer la modélisation de la cible en considérant ses interactions avec le milieu .

  2.3.Le phénomène d'ignition                                           

On n’a pas encore tenu compte du fait que les produits de la réaction interagissent avec le milieu.

2.3.1.Les pertes d’énergie par radiation

                        La cible étant quasiment sous vide, la seule cause de perte est celle par rayonnement de freinage des électrons sur les ions du plasma :c’est ce que l’on appelle le Brehmstrahlung . En fait, l’électron est accéléré par la force coulombienne qui l’attire vers l’ion et comme une charge accélérée rayonne, il s’en suit l’émission d’un photon quasiment dans la direction de la vitesse initiale de l’électron.

            D’où P_b = (4/3)πC_b n² r³ T^1/2 = C_b’ (ρ/<m_i>)² r³ T^1/2 = C_b’’ (ρr)² r T^1/2

                        Ainsi , nous disions au paragraphe précédent (partieA2-2-) que pour obtenir des gains de cible importants, il fallait choisir un paramètre (ρr) le plus grand possible mais on voit qu’un tel choix augmentera de fait les pertes par rayonnement . On a donc un nouveau facteur limitant avec lequel il faudra compter. Un compromis devra être trouvé. De plus à  (ρr) et T fixés, les pertes augmenteront avec la taille de la cible ;là encore un compromis de taille de cible devra être choisi (d’autant plus qu’on verra plus tard que si le gain augmente avec la taille de la cible , certaines instabilités dangereuses commandent ,elles, de limiter la taille de la cible).

2.3.2.Les gains

            Enfin, les neutrons et les alphas produits par la réaction interagissent avec le milieu environnant, y laissant une part de leur énergie.On ne peut réaliser une modélisation convenable de l'implosion de la cible sans en tenir compte.

            Les neutrons n’étant pas chargés électriquement ne subissent aucune interaction coulombienne ; par conséquent leur libre parcours moyen au sein du combustible est très grand et nous admetterons qu’ils n’y laissent quasiment aucune énergie. Une future exploitation industrielle se servira bien évidemment de cet état de fait pour récupérer une partie de l'énergie dégagée par cette fusion : les neutrons étant capable de s'extraire de la cible sans y déposer leur énergie, celle ci pourra être récupérée par un fluide caloporteur approprié.

                  En revanche les alphas interagissent de façon coulombienne avec le milieu et y laissent une grande partie de leur énergie d’où un nouveau facteur de perte d’énergie. Soit λ le libre parcours moyen des alphas ; la probabilité de capture s’exprime alors par :

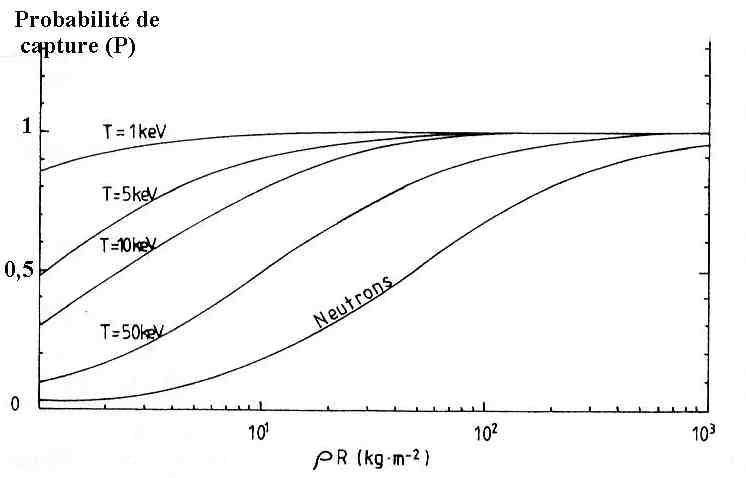
                                               P(α) = 1 – 1/ (1 + r/λ)

Probabilité de capture des alphas (et de neutrons) en fonction du paramètre de cible ρR pour différentes températures

Introduction à la fusion par confinement inertiel , Dautray et Watteau, Eyrolles 1993

            On comprend qu’en fait cette énergie n’est pas perdue car elle contribue à chauffer le combustible jusqu’aux conditions de fusion. Elle permet en définitive de compenser les pertes par rayonnement et le refroidissement dû à l’effet de détente . La température du milieu va donc augmenter et ce de façon exponentielle , par conséquent le taux de réaction croît et le gain G₃ par la même occasion . Ce régime d’entretien de la réaction est appelé régime d’ignition, qui n’apparaît qu’au dessus d’un certain seuil (dépendant de la taille de la cible, des conditions de température et de densité et  de l’énergie des alphas).

            C’est donc ce seuil d’ignition qu’il faut chercher à atteindre pour que la sphère brûle plus vite qu’elle ne se détend : c’est ce régime particuliers et lui seul qui nous donne un espoir de pouvoir brûler du DT en laboratoire avec un gain notable d’énergie.

            Les deux courbes suivantes illustrent bien tout l’intérêt de ce phénomène :

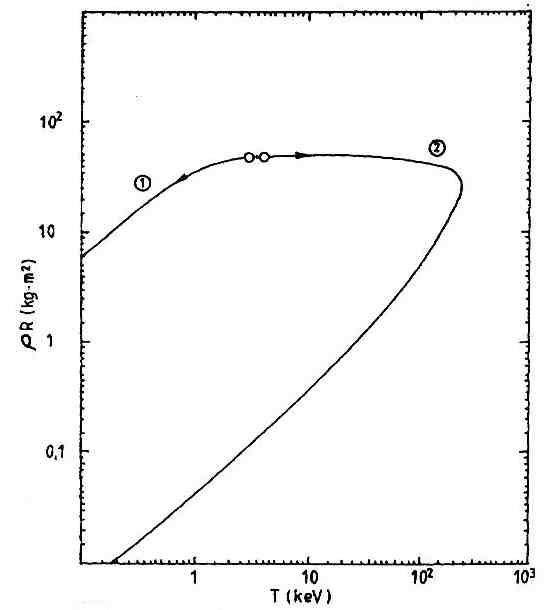	La partie 1 de la courbe est le cas sans ignition  La partie 2 est le cas avec ignition On voit notamment sur cette figure qu’il est inutile de porter initialement le mélange à une température trop élevée car une fois l’ignition atteinte, le mélange monte de lui même en température et brûle. Par exemple pour ρR = 40 kg/m2 environ, il suffit de porter le mélange à 5 ou 6 kev pour que le mélange monte de lui mçme et grâce à l'ignition à plus de 100 keV
Le phénomène d'ignition
Introduction à la fusion par confinement inertiel , Dautray et Watteau, Eyrolles 1993

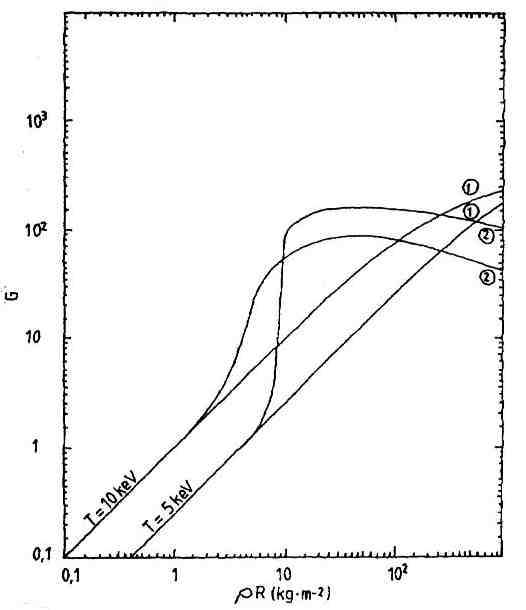	La partie 1 de la courbe est le cas sans ignition  La partie 2 est le cas avec ignition     On voit ici clairement la hausse de gain apportée par la prise en compte de la capture des alphas. Il sera en particuliers inutile d’atteindre des valeurs de ρR trop élevées.
Hausse de gain de cible (G3) lors du phénomène d'ignition
Introduction à la fusion par confinement inertiel , Dautray et Watteau, Eyrolles 1993

          Ce phénomène permet donc de diminuer l’énergie à investir. Pourtant on ne pourra jamais atteindre des gains de cible G₃ supérieur à 200 d’où une exploitation industrielle non rentable ! On est donc amener à choisir des configurations de cibles plus avantageuses. 

2.4.Structure de cible à point chaud                                   

   2.4.1.Intérêt

                        On vient de voir que même en portant une sphère de DT aux conditions de Température et de densité les plus favorables grâce au phénomène d’ignition , il est cependant impossible d’obtenir des gains suffisants à une exploitation industrielle. L’idée consiste donc à ne porter qu’une fraction du mélange aux conditions d’ignition (typiquement quelques pourcents).

Ce sont les alphas qui amèneront le reste du mélange à fusionner en lui transmettant la totalité de leur énergie. On voit là apparaître la nécessité d’une couronne de DT autour du point chaud qui soit suffisamment dense pour capter la totalité de l’énergie des alphas. Cette couronne devra dans le même temps rester froide afin que sa pression cinétique interne ne s’oppose pas à sa compression.

2.4.2.Schéma de cibles réelles

Le schéma de cible suivant résume l’ensemble des contraintes à imposer à la forme de la cible :

• combustible central formé de DT gazeux et dont une partie seulement sera porter aux conditions d’ignition par une loi de poussée du laser appropriée (cf partieB-2-3-2) : taille caractéristique de l’ordre de 80 μm , le point chaud n’excédant pas 40 μm .
• couronne de DT solide sous forme cryogénique d’une quarantaine de μm et qui sera portée à très haute densité par implosion due à l’éclairement laser et ce pour les raisons exposées précédemment et dont le détail de l’étude sera l’objet de la partie B.
• Un ablateur de CH solide (plastique) dopé par un matériau lourd opaque aux rayons X d’environ  10 μm et dont le rôle est de faire office de piston lors de la compression de la cible (cf partieB-2)

	Structure de la cible cryogénique     R.Goutallier 2001
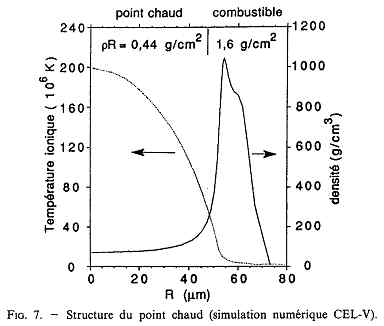	Structure du point chaud : le point chaud est crée dans une zone peu dense (DT gazeux) et l'énergie de fusion ainsi libérée est en partie déposée par les alphas dans une couronne très dense de DT solide dont la compression a été préallablement réalisée par la mise en vitesse centripète progressive de l'ablateur externe sous l'impulsion mise en forme de lasers de puissances (1,8 MJ)

              En deux mots, l’usinage des cibles est assez complexe et mériterait à lui seul un dossier . En effet de leur confectionnement  rigoureux dépend la bonne marche de l’expérience et l’obtention de gains élevés ; on va voir qu’il est indispensable d’avoir des sphères concentriques les plus parfaites possibles pour limiter les instabilités de plasma (cf partieB-3).

                 Le microballon de CH est rempli par diffusion d’un mélange de gaz DT sous forte pression ; le DT est ensuite gelé dans un cryostat, où une circulation d’hélium liquide abaisse la température, pour former une couche homogène fine sur la paroi intérieure. On peut citer à ce stade un problème ( de taille) qui rendra encore plus complexe l’usinage des cibles : cette couche de DT cryogénique est rendue inhomogène sous l’effet de la pesanteur. On utilise un procédé de chauffage qui permet de lisser et d’uniformiser plus ou moins bien ce dépôt.

                        Après avoir vu comment obtenir des gains permettant de rentabiliser une application industrielle et en avoir déduit la structure à donner à la cible , nous allons nous intéresser de plus près à la compression du mélange proprement dit et à la façon de créer le point chaud . Nous verrons les différents problèmes rencontrés au cours du processus d’utilisation de l’énergie laser pour l’implosion.

N'hésitez pas à m'écrire pour des critiques (constructives) ou des renseignements